Прежде чем приводить формулы для площади, вспомним несколько основных понятий.
Треугольник можно назвать одной из простейших геометрических фигур. Он образуется, если соединить три не лежащие на одной прямой точки отрезками. Эти отрезки называются сторонами треугольника, а сами эти точки, в которых сходятся отрезки — вершинами треугольника.
Очень часто вершины треугольника обозначают как А, В, С, а стороны как a = BC, b = AC, c = AB.

Высотой (h) треугольника называют перпендикуляр, опущенный из вершины на противолежащую ей сторону, либо на ее продолжение (если треугольник тупоугольный). Так как в треугольнике 3 вершины, то и высот тоже 3.
Площадь треугольника Δ ABC (обозначается как SABC) — это число, показывающее, сколько единиц площади (квадратных метров, сантиметров и т.д.) содержится в фигуре. Кроме того, площадь треугольника — это та часть плоскости, которая окружена тремя сторонами этого треугольника.
Для вычисления площади треугольника можно использовать несколько разных формул.
Формула площади треугольника через сторону и высоту
Это самая простая формула. Согласно этой формуле, чтобы найти площадь треугольника, нужно умножить длину стороны на длину высоты, опущенной на нее, и разделить полученное произведение на 2.
Так, если высота h треугольника опущена на a, то формулу, по которой вычисляется площадь, можно записать следующим образом:
S = h • a / 2.
Ее обычно зачитывают как: «половина произведения основания на высоту».
Формула площади треугольника через две стороны и угол между ними
Если в треугольнике известны длины, которые имеют две его стороны, и величина угла между ними, то можно найти его площадь, сначала умножив длины сторон треугольника друг на друга и на синус угла и затем разделив полученное произведение на 2.
S = (a • b • sin γ) / 2.
В случае равностороннего треугольника эта формула приобретает вид:
S =√3 • a2 / 4. Знать ее очень полезно.
Если известна только одна сторона треугольника и все углы, то для расчета площади можно воспользоваться следующей формулой:
S = a2 • sin β • sin γ / (2 • sin α).
Площадь произвольного треугольника через три стороны. Формула Герона
Если известны длины всех трех сторон, то найти площадь можно, используя универсальную формулу Герона. Греческий математик Герон Александрийский вывел ее примерно в 60 г. н. э. В современной записи она выглядит следующим образом:

где p — это полупериметр треугольника, вычисляемый по формуле:
p = (a + b + c) / 2.
Формулу Герона очень легко запомнить, так как в ней используются стороны, но нет ни синусов, ни косинусов углов. Хоть вычисления площади весьма громоздкие, но знать эту формулу полезно.
Через радиус описанной окружности
Если известен радиус описанной окружности R и длины сторон треугольника, то для расчета площади удобно пользоваться следующей формулой:
S = a • b • c / (4 • R).
Через радиус вписанной окружности
Площадь треугольника через радиус r вписанной окружности выражается следующей формулой:
S = r • (a + b + c) / 2.
А так как (a + b + c) / 2 — это полупериметр треугольника, то площадь можно записать в виде более компактной формулы (произведение радиуса вписанной окружности на полупериметр):
S = r • p.
Через сторону и два прилежащих к ней угла
Для случая, когда известна одна сторона треугольника и два прилежащих к ней угла, есть следующая формула для расчета площади:
S = a2 • sin β • sin γ / (2 • sin (β + γ)).
Итак, мы имеем три очень полезные и похожие друг на друга формулы для расчета площадей через длины сторон и значения углов треугольника:
- S = (a • b • sin γ) / 2;
- S = a2 • sin β • sin γ / (2 • sin α);
- S = a2 • sin β • sin γ / (2 • sin (β + γ)).
Частные случаи
Формулы для равнобедренных треугольников, позволяющие найти площадь, приобретают следующий вид:

S = a2 • sin β / 2;
S = a • b • sin α / 2;
S =b2 / (4 • tg (β / 2).
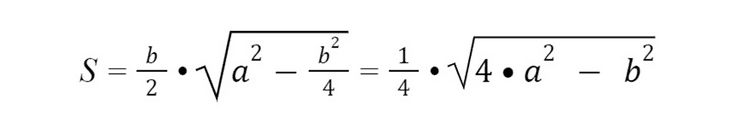
Для нахождения площади через радиус описанной окружности и две стороны имеем:
S = a2 • b / (4 • R).
Площадь треугольника, все стороны которого имеют одинаковую длину, можно вычислить значение следующим образом:

Формула вычисления площади через радиус описанной окружности приобретает вид:
S = a3 / (4 • R).
Умение быстро вычислять площадь треугольника необходимо для успешной сдачи ОГЭ и ЕГЭ по математике базового уровня. Среди вариантов контрольных и экзаменов попадаются задачи следующих типов.
Пример №1. Найдите площадь треугольника АВС, одна сторона которого равна 8 см, другая 14 см, а угол между ними равен 30°.
Решение будет следующим:
S = 8 • 14 • sin (30°) / 2.
S = 8 • 14 • 0,5 / 2.
S = 28 кв. см.
Пример №2. Найдите площадь треугольника АВС, если одна из его сторон равна 20 см, а высота равна 40 см.
Решение:
S = 20 • 40 / 2.
S = 400 кв. см.
Пример №3. Вычислите площадь прямоугольного треугольника, один катет которого равен 15 см, а другой — 30 см.
Решение:
Вспоминаем, что катет прямоугольного треугольника одновременно является и высотой, поэтому площадь данного треугольника будет равна:
S = 15 • 30 / 2.
S = 225 кв. см.
Пример №4. В треугольнике АВС одна сторона (a) равна 4 см, другая (b) равна 20 см. Высота, проведенная к a, равна 10 см. Найти высоту, проведенную к b.
Решение:
В условии даны две стороны Δ АВС, но нет задания «найдите площадь Δ АВС». Но быстро решить задачу можно, как раз воспользовавшись тем, что площадь выражается следующей формулой:
S = ha • a / 2 = hb • b / 2.
Следовательно:
hb = ha • a / b.
hb = 4 • 10 / 20 = 2 см.
Пример №5. В прямоугольном треугольнике Δ АВС длина одного из катетов равна 8 см. Противолежащий этому катету угол равен 45°. Вычислите площадь треугольника Δ АВС.
Решение:
Зная один острый угол в прямоугольном треугольнике, мы можем вычислить второй. Он будет равен 180° - 90° - 45° = 45°. Следовательно, данный прямоугольный треугольник АВС является равнобедренным, что существенно упрощает вычисления.
S = 8 • 8 / 2.
S = 32 кв. см.
Пример №6. В прямоугольном треугольнике Δ АВС катет равен 7 см, а гипотенуза — 25 см. Найти SABC.
Решение:
Длину второго катета прямоугольного треугольника найдем с помощью теоремы Пифагора.
b2 + 72 = 252.
b = 24.
Теперь, когда известны оба катета, находим площадь SABC.
SABC = 7 • 24 / 2 = 84 кв. см.



